化合物の立体表記方法 - 破線－くさび形表記・ニューマン投影式・フィッシャー投影式

立体表記の必要性

化合物は原子が3次元的に結合したものです。したがって、その形を2次元の紙面上の図に正確に表現することはできません。

しかし、化学を学ぶ上で、鏡像異性体（エナンチオマーやジアステレオマー）や回転異性体のような立体異性体の区別が重要になる場合があります。

それは、このような異性体同士の性質が異なっていたり、生体に対して異なる反応をしたりするためです。また、化学反応の過程で、分子の立体配置がどのように変わるのかというのも重要な点になります。

このような異性体を表現するために、2次元の紙面上にその立体配置を表現する必要性が生じます。

例えば、エナンチオマーやジアステレオマーを区別するには、破線－くさび形表記やフィッシャー投影式を用います。破線－くさび形表記は視覚的に分かりやすい表記方法で、構造式を書くのによく用いられます。一方のフィッシャー投影式は、より簡潔な表記法であり、多数の不斉炭素原子を持つ場合などに便利な表記です。

回転異性体を区別するためにはニューマン投影式を用います。

破線－くさび形表記

破線－くさび形表記（英語：dashed-wedged line drawing, zig-zag projection）では、通常の実線でつながれた原子は紙面（画面）上の2次元空間にあるものとし、それに対して、紙面の手前に出ている原子をくさび形で、紙面の奥に出ている原子を破線でつなぎます。

この表記方法は、最も頻繁に使われる分子の立体表記方法です。

例として、乳酸分子を見てみましょう。下に示した乳酸分子の中心の炭素原子には、4つの異なる原子や原子団がついています。このような炭素原子を、不斉炭素原子と呼びます。

上の表記では、2つの鏡像異性体のうち、どちらであるか分かりません。

この立体異性体を区別するために、破線－くさび形表記を用います。中心の炭素原子に結合する4つの原子は、四面体を作っていることを思い出してください。

このようにして破線－くさび形表記を用いることで、鏡像異性体を区別することができます。

なお、上の乳酸分子は、左側がR体、右側がS体と呼ばれるものです。

フィッシャー投影式

フィッシャー投影式（英語：Fischcer projection formula）は、十字で表された構造式の中心に不斉炭素原子が位置するものとし、その上下に位置する原子は紙面の奥に、左右に位置する原子は紙面の手前に出ているものとして表現する方法です。

すなわち、次のフィッシャー投影式は、右の破線－くさび形表記と同じ意味です。

例として、上の破線－くさび形表記の説明に用いた乳酸分子の2つの鏡像異性体を、フィッシャー投影式で表してみましょう。

上の3つの表記が同一のものであること、確認できたでしょうか？頭の中で立体を動かして考えてみてくださいね。

さて、フィッシャー投影式は、破線－くさび形表記を簡略化したものであり、糖などの不斉中心を多数持つ分子の表現に便利です。

次の図は、鎖状D－グルコースのフィッシャー投影式です。このような長鎖分子を書くときは、一般に炭素主鎖が縦になるように書きます。

ニューマン投影式

ニューマン投影式（英語：Newman projection formula）では、注目する2原子の結合軸の延長上から分子を眺め、結合軸に垂直な平面へ各置換基を投影します。注目する2原子は重なって見えます。このうち、奥側の原子に結合する基を円周から引いた線で、手前の原子に結合する基を円の中心から引いた線で表します。

ニューマン投影式は、隣接する2原子に結合する置換基の相対的な位置関係を表すための方法です。回転可能な単結合の、その回転角に対するポテンシャルエネルギーを考える場合に利用されます。

といわれてもピンと来ないと思いますので、例として、エタン分子を2つの炭素の結合についてニューマン投影式で表してみましょう。

ここで、重なり形配座では前後の原子に結合する置換基は重なっているのが本当の姿です。しかし、絵でもそのように描くと、原子がごちゃごちゃしてしまうので、若干回転角をずらして書いています。

ねじれ形と重なり形の分子模型を次に示します。水素原子の位置関係について、確認してください。

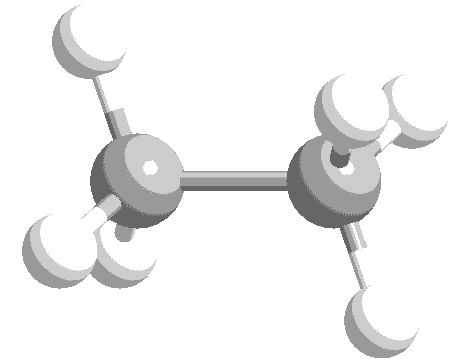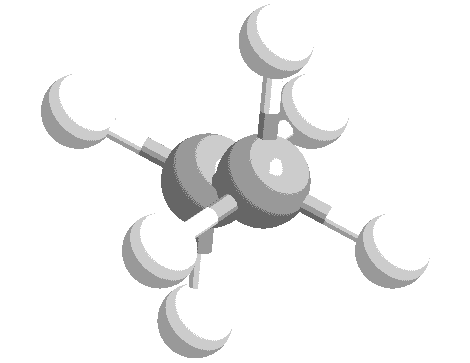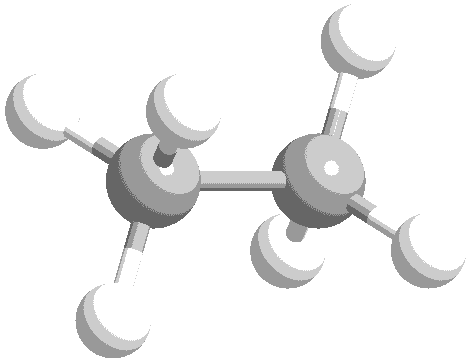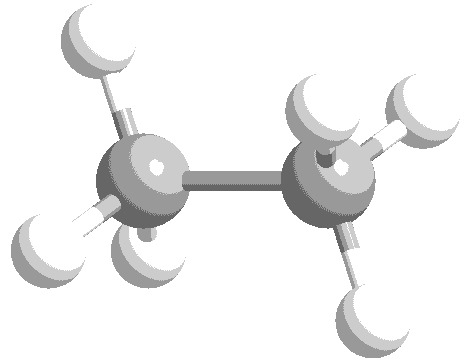
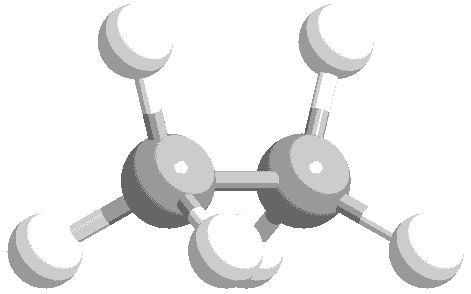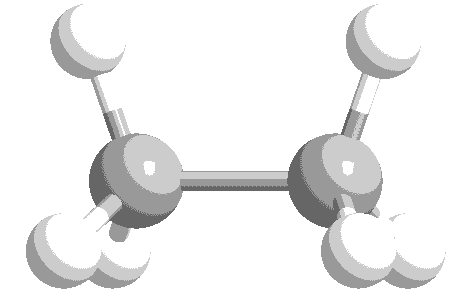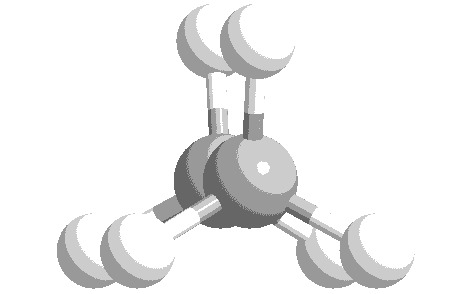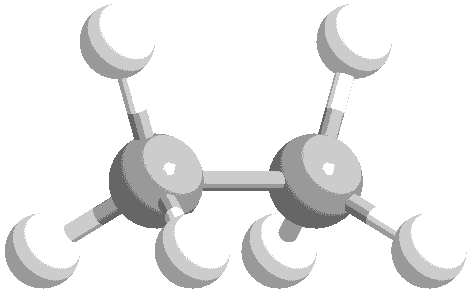
このような、単結合の回転角の違いによる異性体を回転異性体と言います。

実際には、エタン分子の重なり形は、ねじれ形に比べて不安定な配座です。したがって、全体の約99％はねじれ形として存在し、残り約1パーセントが重なり形として存在しています。

このように、C－C単結合は回転可能ではありますが、基本的に立体障害が最も少ない配座が安定となります。こういった回転異性体の安定性を議論する際に、ニューマン投影式が利用されます。