微分の公式一覧
このページでは、関数 $ f(x) $ を微分して得られる導関数 $ f'(x) $ の基本的な公式を掲載しています。また、 和や差、積、商の微分公式や合成関数の微分公式なども掲載しています。
導出方法はみなさん自身でご確認の上、公式を確認してくださいね。
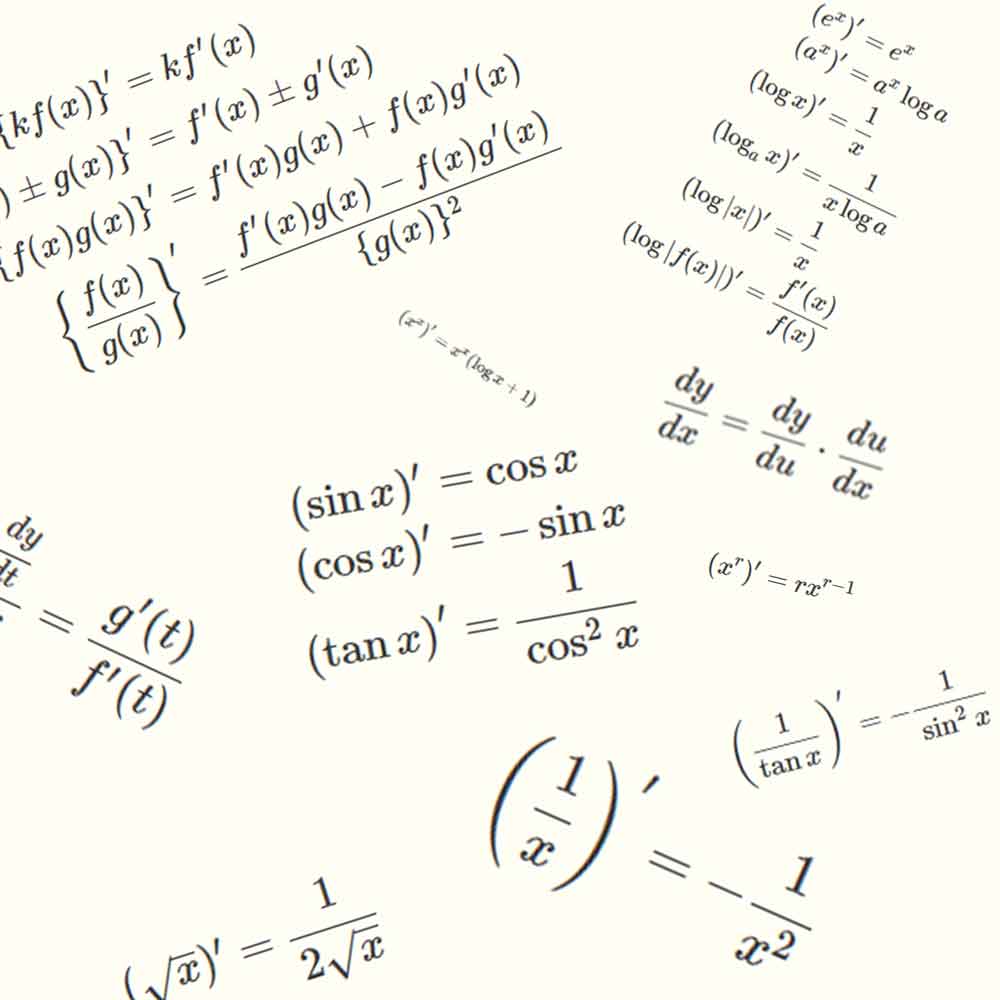
もくじ
高校レベルの微分公式
導関数の定義
関数 $ f(x) $ を微分して得られる導関数 $ f'(x) $ は次式で定義される。
\begin{align*} f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h} \end{align*}
そもそも、微分の意味ってなんだっけ?という方は、「微分とは何か? - 中学生でも分かる微分のイメージ」をご覧になってください。
初等関数の微分公式
xr(べき乗)の微分
xr(べき乗)の導関数は次の通りです。
$ r $ が有理数のとき
\begin{align*} (x^r)' &= r x^{r-1} \end{align*}
とくに、$ r = \frac{1}{2} $ のとき
\[ ( \sqrt{x} )' = \frac{1}{2\sqrt{x}} \]
また、$ r = -1 $ のとき
\[ \left( \frac{1}{x} \right) ' = - \frac{1}{x^2} \]
三角関数の微分
三角関数(sin, cos, tan)の導関数は次の通りです。
\begin{align*} (\sin x )' &= \cos x \\[5pt] (\cos x)'& = - \sin x \\[5pt] \left( \tan x \right)' &= \frac{1}{\cos^2 x} \\[5pt] \end{align*}
タンジェントの微分については、後に示す商の微分公式から求めることが出来ます。
ちなみに、
\begin{align*} \left(\frac{1}{\tan x} \right)' &= - \frac{1}{\sin^2 x} \end{align*}
sin x と cos x の第 n 次導関数は次の通りです。
\begin{align*} \left(\sin x \right)^{(n)} &= \sin \left( x + \frac{1}{2}n \pi \right) \\ \left(\cos x \right)^{(n)} &= \cos \left( x + \frac{1}{2}n \pi \right) \end{align*}
指数関数・対数関数の微分
指数関数と対数関数(log)の導関数は次の通りです。
\begin{align*} \left(e^x\right)' &= e^x \\[5pt] (a^x )' &= a^x \log a \\[5pt] (\log x )' &= \frac{1}{x} \\[5pt] (\log_a x)' &= \frac{1}{x \log a} \\[5pt] (\log |x| )' &= \frac{1}{x} \\[5pt] (\log |f(x)| )' &= \frac{f'(x)}{f(x)} \\[5pt] \end{align*}
log x の第 n 次導関数は次の通りです。
\[ (\log x)^{(n)} = \frac{(-1)^{n-1}(n-1)!}{x^n} \]
様々な関数の微分公式
線形性と積や商の微分
関数の定数倍や和、差の微分について、関数 $ f(x) , g(x) $ が微分可能なとき
\begin{align*} \left\{ kf(x) \right\} ' &= kf'(x) \\[5pt] \left\{ {f(x) \pm g(x)}\right\}' &= f'(x) \pm g'(x) \\[5pt] \end{align*}
ただし $ k $ は定数である。
関数の積や商の微分は次の通りです。
\begin{align*} \left\{ {f(x)g(x)}\right\}' = f'(x)g(x) + f(x)g'(x) \\[5pt] \left\{ {\frac{f(x)}{g(x)}}\right\}' = \frac{f'(x)g(x) - f(x)g'(x)}{\{g(x)\}^2} \\[5pt] \end{align*}
最後に示した商の微分において、とくに $ f(x) = 1 $ のとき
\begin{align*} \left\{ {\frac{1}{g(x)}}\right\}' &= - \frac{g'(x)}{\{g(x)\}^2} \\ \end{align*}
合成関数の微分
微分可能な関数 $ y = f(u), u=g(x) $ の合成関数 $y=f(g(x))$ の導関数は
\begin{align*} \frac{dy}{dx} &= \frac{dy}{du} \cdot \frac{du}{dx} \\ \end{align*}
逆関数の微分
\begin{align*} \frac{dy}{dx} &= \frac{1}{\frac{dx}{dy}} \\ \end{align*}
ただし $ \frac{dx}{dy} \neq 0 $
媒介変数表示された関数の微分
$ x=f(t), y=g(t) $ のとき
\begin{align*} \frac{dy}{dx} &= \frac{\frac{dy}{dt}}{\frac{dx}{dt}} = \frac{g'(t)}{f'(t)} \\ \end{align*}
対数微分法
公式ではありませんが、両辺の対数を取ってから微分する方法です。
これを用いると、たとえば
\begin{align*} \left( x^x \right)' = x^x (\log x + 1) \\ \end{align*}
となります。
上式は、$ y=x^x $ とおいてから両辺の対数を取り、その両辺を $x$ で微分することで得られます。
大学レベルの微分公式
逆三角関数と双曲線関数の微分
逆三角関数の微分
\begin{align*} \left( \arcsin x \right)' &= \frac{1}{\sqrt{1-x^2}} \\[5pt] \left( \arccos x \right)' &= - \frac{1}{\sqrt{1-x^2}} \\[5pt] \left( \arctan x \right)' &= \frac{1}{1+x^2} \\[5pt] \end{align*}
双曲線関数の微分
\begin{align*} \left( \sinh x \right)' &= \cosh x \\[5pt] \left( \cosh x \right)' &= \sinh x \\[5pt] \left( \tanh x \right)' &= 1-\tanh^2 x \\ &= \frac{1}{\cosh^2 x} \\[5pt] \end{align*}
